Optimal Control of Heating During Vacation
Published:
What should your thermostat do when you are away from home? Say you keep the temperature of your home, $x(t)$, at a fixed temperature $H_i$ when you are around. Assume that you are going to be leaving for a winter vacation at time $t=0$, and you want the home to be the same temperature when you return at time $t=T$, but you don’t care about the home’s temperature when you are gone. We will use Pontryagin’s maximum principle to achieve your desired final temperature, while minimizing the amount of energy used while you are gone.
Acknowledgements
This post was inspired by the course Introduction to Control Theory and Optimal Control taught by Nicolas Charon at Johns Hopkins University.
The Control System
A primary influence on the temperature of your home is the outdoor temperature, which we will assume to be constant, $H_o$. According to Newton’s rate of cooling, your home will cool at a rate proportional to $x-H_o$. However, we can warm the home by, say, burning gas in a furnace at a rate $u(t)$. Our control system is then:
\[\dot x(t)=-k(x(t)-H_o)+u(t)\]However we will make a substitution for simplicity $y=x-H_o$:
\[\dot y(t)=-ky(t)+u(t)\]And our endpoint conditions are $y(0)=y(T)=H_i-H_o$. First, we note that we have a linear, homogeneous, autonomous system. Further, the coefficient on $u$ is nonzero so the system is controllable by the Kalman condition. In particular, at any time $T>0$, we can control the system to any state $y$. This means that, for example, no matter what temperature our house is before we get back, it can be controlled to our desired temperature in an infinitely small amount of time.
Goal
Our goal is to minimize the total gas burned during our absence, which is:
\[C(u)=\int_0^T |u(t)|dt\]where the Lagrangian is $L(u)=\vert u(t)\vert$. As mentioned before, the system is controllable at any positive time. Further, it can be shown that the total gas burned, $C$ can be made infinitely small by waiting longer and longer to heat the home back up (and doing so by burning gas at a very high rate $u$). This degenerate problem is not interesting, so we consider a constrained control, $u \in L^\infty([0,T],[0,U])$ i.e. $u$ has a maximal value of $U$. In this case, we have to assume that $U/k>H_i>H_o$, meaning we can burn gas at a rate fast enough to achieve our desired temperature and that our desired temperature is warmer than the outside temperature. I will not focus on the units of $u$ but, each unit $u$ is the rate of energy consumption needed to heat up the home at a rate of $1$ degree per day, when the home is the same temperature as the outdoors.
Solving the Optimal Control Problem
Our Hamiltonian is:
\[H_\lambda(y,p,u)=p(u-ky)-\lambda |u|\]And we can apply the strong Pontryagin maximum principle which is a necessary condition for an optimal control $u$, assuming one exists. The condition for optimality is in the following equations:
\[\begin{align} \dot y &= \nabla_p H_\lambda(y,p,u) \nonumber \\ &= u-ky \\ \dot p &= -\nabla_y H_\lambda(y,p,u) \nonumber \\ &= kp \\ u(t) &= argmax_{v \in [0,U]} \; H_\lambda(y,p,v) \nonumber \\ &= argmax_{v \in [0,U]} \; p(v-ky)+\lambda |v| \nonumber \\ &= argmax_{v \in [0,U]} \; v(p-\lambda) \end{align}\]First, Equation 6 tells us that $p(t)=p(0)e^{kt}$. If $p(0) \leq 0$ then the resulting control would be $u(t)=0$ which will not satisfy the terminal condition (the house would cool below the desired temperature). Thus $p(t)=p(0)e^{kt}$ is always positive. Next, if $\lambda=0$, then this would result in the control $u(t)=U$, which also would not satisfy the terminal condition (the house would be heated to above the desired temperature). So we can assume $\lambda=1$, and that $p(0) < \lambda$, since otherwise the control would again be $u(t)=U$. In this case, the control involves $u=0$ up to some time $t’$, at which point the furnace kicks on at maximal power $U$. Let’s compute the time at which the furnace should kick on by solving for $y$.
\[\begin{align*} y(t) &= y(0)e^{-kt} & 0<t\leq t' \end{align*}\]After time $t’$ we have $\dot y = U-ky$, so we make the substitution $z=y-U/k$ to get $\dot z=-kz$ with the solution $z(t)=z(t’)e^{-k(t-t’)}$ which means:
\[\begin{align*} y(t) &= (y(t')-U/k)e^{-k(t-t')}+U/k & t'<t<T \\ &= (y(0)e^{-kt'}-U/k)e^{-k(t-t')}+U/k \\ &= y(0)e^{-kt}-U/ke^{-k(t-t')}+U/k \\ &= (H_i-H_o)e^{-kt}-U/ke^{-k(t-t')}+U/k \end{align*}\]And in order to satisfy the terminal condition, we have:
\[\begin{align*} H_i-H_o &= (H_i-H_o)e^{-kT}-U/ke^{-k(T-t')}+U/k \\ (H_i-H_o)(1-e^{-kT})-U/k &= -U/ke^{-k(T-t')} \\ 1-\frac{H_i-H_o}{U/k}(1-e^{-kT}) &= e^{-k(T-t')} \\ T+\frac{\log \left(1-\frac{H_i-H_o}{U/k}(1-e^{-kT}) \right)}{k} &= t' \end{align*}\]In other words, the furnace should kick on at maximal power $U$ at a time $-\frac{\log \left(1-\frac{H_i-H_o}{U/k}(1-e^{-kT}) \right)}{k}$ before your time of return (yes, this is a positive quantity, since the argument of the logarithm is below 1 given our assumption $U/k>H_i>H_o$).
Parameter Effects on Heating Time and Energy Consumption
Let’s examine the influence of the different parameters on the time to reheat ($T-t’$) and average energy spent per day ($\int \vert u\vert dt/T$). The parameters we will look at are time spent away ($T$), temperature difference between outside and inside ($H_i-H_o$), maximum heating power ($U$), and cooling rate ($k$). When a parameter is not being varied, it takes its default value of $T=7$ days, $H_i-H_o=35$ F, $U=24$, $k=0.34 \; \text{day}^{-1}$. The default value of $k$ means the temperature difference between the house and the outdoors cuts in half roughly every two days, which seems reasonable. The default value of $U$ means the maximal temperature that the furnace can heat the house is $100$ degrees, which also seems reasonable.
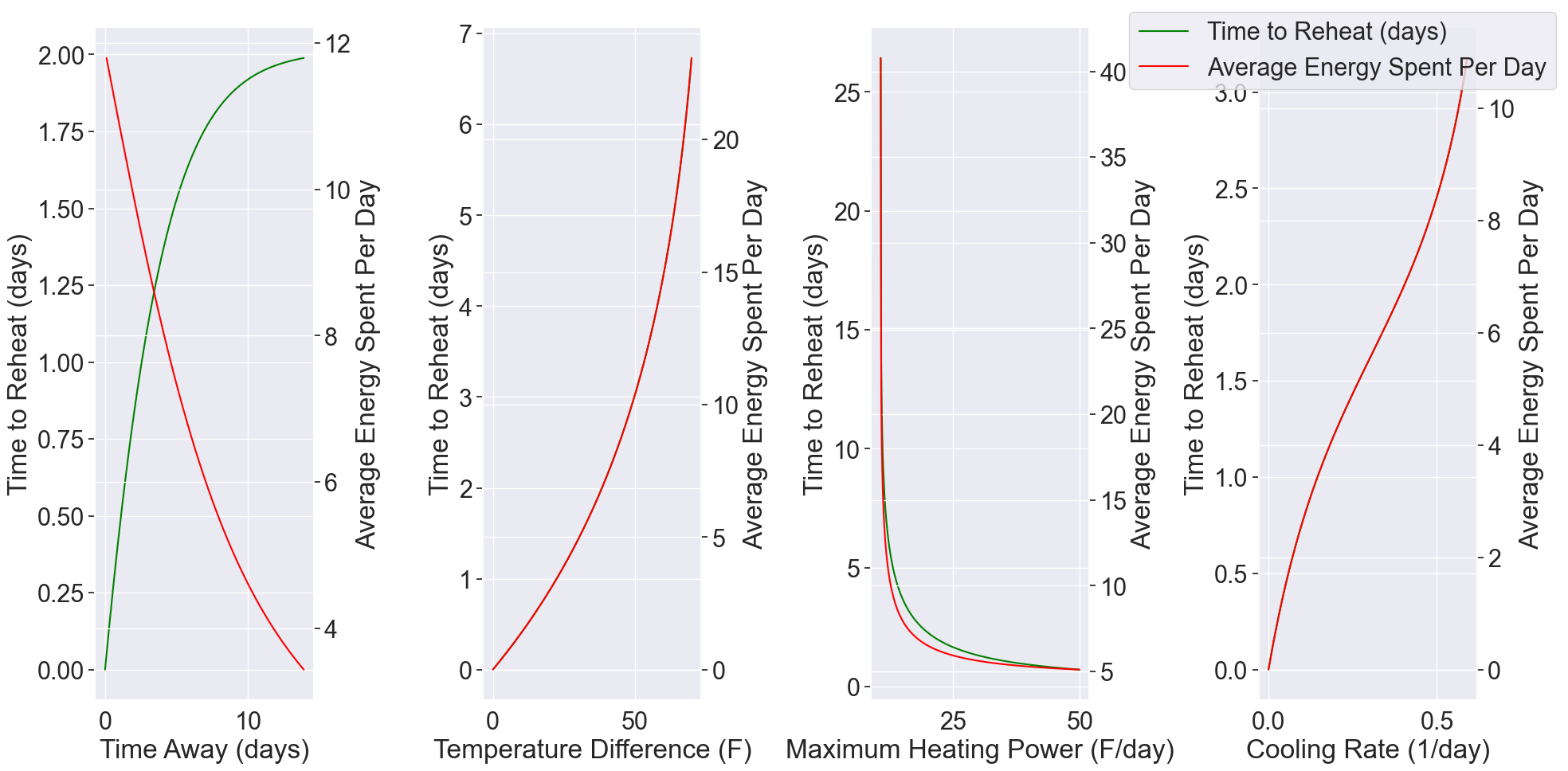
The results are mostly intuitive. First of all, faster cooling rate or higher temperature difference between inside and outside requires more average energy used and more advanced time to reheat the home. A higher maximum heating power shortens the heating time, but also perhaps unintuitively lowers the amount of total energy used (this is related to the degenerate unconstrained problem mentioned earlier). Lastly, the longer you are away means your furnace needs more time to reheat, but overall less average energy consumed per day - so for the sake of energy consumption, take a vacation!
Assumptions
This analysis relies on a model of your home’s temperature which is, of course, wrong. Among the assumptions which may or may not matter in the real world are:
- Constant outdoor temperature $H_o$
Of course, outdoor temperatures fluctuate with weather systems, and day/night. However this shouldn’t really change the strategy, as long as you can dynamically compute how much time your home will need to heat up, and that the outdoor temperature is roughly constant while the home is reheating.
- Your heater has constant efficiency across its operating range
This is probably false, but I am not an HVAC expert enough to know the extent to which this is false. But it is likely that at high power, the furnace is less efficient, just like a car going at high speeds. This could change the nature of our control because it might be more useful to exploit the most efficient window of operation. However, absent any further information about how furnaces operate, I am not able to include this in my model.
