Cursory Mathematical Analysis of MYHockey Rankings Algorithm
Published:
I recently move to Massachusetts where the youth sport of choice is ice hockey. I was watching my cousin play a game and, between the crashes of body checks into the boards that made me fear for my cousin’s life, my uncle told me about a website where he gets his intel on the other teams - myhockeyrankings.com.
From what I can understand, the website was developed about 20 years ago by some hockey parent(s) who wanted to quantitatively compare teams that didn’t play each other. The key assumption of this system is that a team’s strength can be approximated with a single number, their “Rating.” Since numbers are ordered, this means that if team A is better than team B and team B is better than team C, then team A should be better than team C. Of course some enthusiasts will object because this does not leave room for a scenario where team C’s playing style happens to expose the weaknesses of team A. However I will no focus on this question. I will assume that this central assumption is true, my goal is to better understand how game scores influence ratings via the given formula.
According to a post on their website, a team’s rating is computed to be the sum of their “Sched” score (the average strength of their opponents), and their “AGD” (average goal differential, with a single game differential capped at 7). Some details of their algorithm are not explicitly clear to me (e.g. Does the Sched score only include opponents that have already been played that season or does it include future opponents? Is the Sched score computed using ratings at the end of last season or are these ratings updated throughout the season?). Nevertheless, I was tempted to do some mathematical analysis.
We will examine how current ratings are computed. We will assume:
- Sched scores only include opponents that have already been played that season
- Sched scores are based on ratings from the previous year.
I looked at the Math page of some hockey teams on the site, and what I saw there supports both of these assumptions.
If there are $D$ teams in a league, let $r \in \mathbb{R}^D$ be the vector of ratings for each of the teams where $r_i$ is the rating of team $i$:
\[\begin{align*} r=\begin{pmatrix} r_1 \\ r_2 \\ ... \\ r_D \end{pmatrix} \end{align*}\]We will denote the ratings at the end of the previous year as $r^{(prev)}$.
Then, let $S$ be the matrix that contains schedule information. Element $S_{ij}$ is the number of times that team $i$ played team $j$ this season. As an example, in a league with 4 teams, say team 1 played team 2, and team 3 played team 4. Then, our $S$ matrix is:
\[\begin{align*} S=\begin{pmatrix} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix} \end{align*}\]Next, let $\Delta$ be the vector of goals scored minus goals yielded for each team. For example, if team $i$ scored 5 goals and yielded 2 goals, then $\Delta_i=3$. We will examine this system under a variety of settings, starting with a simple setting.
Setting 1) Each team plays $n$ games, no scoring cap
In this case, the Sched score is given as $\frac{1}{n}Sr^{(prev)}$ and the AGD score is $\frac{1}{n}\Delta$, so the current ratings formula is:
\[\begin{align*} r&=\frac{1}{n}(Sr^{(prev)}+\Delta) \end{align*}\]Result 1a) When does a rating increase or decrease?
If we examine the quantity $r - r^{(prev)}$, we get the following formula:
\(\begin{align} n*\left(r_i-r_i^{(prev)}\right) &= \Delta_i - \left(\sum_{\text{games played by team }i} r_i^{(prev)} - r_{\text{opponent in game }g}^{(prev)} \right) \end{align}\) Or, in words: \(\begin{align*} n*\text{(rating change)} &= \text{goal diff} - \left(\sum_{g \in games} \text{ prev. rating} - \text{rank of opponent} \right) \end{align*}\)
Proof:
\[\begin{align*} r - r^{(prev)}&=\frac{1}{n}Sr^{(prev)} + \frac{1}{n}\Delta - r^{(prev)} \\ &=(\frac{1}{n}S-I)r^{(prev)} + \frac{1}{n}\Delta \\ n(r - r^{(prev)})&=(S-nI)r^{(prev)} + \Delta \end{align*}\]The $i$’th term in the last line above is given as:
\[\begin{align*} n(r_i - r^{(prev)}_i)&=\Delta_i - \left(\sum_{g \in \text{games played by team }i} r^{(prev)}_i-r^{(prev)}_{\text{opponent in game g}}\right) \\ \end{align*}\]$\blacksquare$
So a team’s rating will be unchanged if their goal differential is precisely the rating difference between them and their opponents . If they score more goals than this rating difference, their rating will increase, otherwise it will decrease.
Result 1b) Conservation of total rating
Another observation in this setting is that the sum of the ratings remains unchanged
\[\begin{align} \sum_i r_i=\sum_i r^{(prev)}_i \end{align}\]Proof:
First we rewrite $\sum_i r_i$ as $1^Tr$, which is more concise.
\[\begin{align*} 1^T r&=\frac{1}{n}1^T(Sr^{(prev)}+\Delta) \\ &=\frac{1}{n}(1^TSr^{(prev)}+1^T\Delta) \\ &= \frac{1}{n}(n1^Tr^{(prev)}+0) &\text{Each team plays $n$ games, and the goal differentials sum to 0} \\ &= 1^Tr^{(prev)} \end{align*}\]$\blacksquare$
Setting 2) Teams play a variable amount of games, no scoring cap
In this case, we need to normalize ratings by different numbers $n_i$, the number of games that team $i$ has played. The vector that contains these values is $n$, and we introduce the $diag(\cdot)$ operator, which takes a vector, and produces a corresponding diagonal matrix whose diagonal entries are given by the vector. Our new update rule is:
\[\begin{align*} r&=(diag(n))^{-1}(Sr^{(prev)} + \Delta) \end{align*}\]Note that $n=S1$ where $1$ is the vector of all 1’s.
It turns out that the rule for whether a rating increases/decreases is the same, it is related to whether a team’s goal differential is more or less than its cumulative rating differential.
\[\begin{align} n_i(r_i-r_i^{(prev)})&=\Delta_i - \sum_{g \in \text{games played by team }i} \left(r^{(prev)}_i-r^{(prev)}_{\text{opponent in game g}}\right) \\ \end{align}\]Result 2a) Random Games Scores
We have already shown that when goal differentials match rating differentials, ratings are unchanged. This property extends to a stochastic setting as well. If, for every pair of teams $i,j$, games between them result in a random goal difference that is independent and identically distributed with expected value equal to $r_i^{(prev)}-r_j^{(prev)}$, then, as the number of games between all pairs of teams either goes to infinity or stays at zero, the ratings will converge to the same ratings as the previous year.
Proof:
Let’s expand $\Delta_i$:
\[\begin{align*} \Delta_i &= \sum_{j \in \text{opponents of team }i} \sum_{g \in \text{games against }j} \delta_g \\ &= \sum_{j \in \text{opponents of team }i} n_{ij}\left( \frac{1}{n_{ij}}\sum_{g \in \text{games against }j} \delta_g\right) \end{align*}\]where $\delta_g$ is the goal difference between team $i$ and $j$ in game $g$. If each $\delta_g$ is independent and identically distributed with expected value equal to the teams’ rating difference $r_i^{(prev)}-r_j^{(prev)}$, then:
\[\begin{align*} \lim_{n_{ij}\rightarrow \infty \forall i,j} \Delta_i &= \sum_{j \in \text{opponents of team }i} n_{ij}\left( r_i^{(prev)}-r_j^{(prev)}\right) \end{align*}\]and we plug this into the rank change formula:
\[\begin{align*} n_i(r_i-r_i^{(prev)})&=\sum_{j \in \text{opponents of team }i} n_{ij}\left( r_i^{(prev)}-r_j^{(prev)}\right) - \sum_{g \in \text{games played by team }i} \left(r^{(prev)}_i-r^{(prev)}_{\text{opponent in game g}}\right) \\ &= \sum_{j \in \text{opponents of team }i} n_{ij}\left( r_i^{(prev)}-r_j^{(prev)}\right) - \sum_{g \in \text{games against }j}\left(r^{(prev)}_i-r^{(prev)}_{\text{opponent in game g}}\right) \\ &= 0 \end{align*}\]$\blacksquare$
However, the sum of the ratings is no longer conserved, instead a different quantity is conserved:
\[n \cdot r = n \cdot r^{(prev)}\]Result 2b) Example where rating sum is not conserved
\[\begin{align*} r^{(prev)} &= \begin{pmatrix} 1 \\ 0 \\ 0 \\ -1 \end{pmatrix}, S &= \begin{pmatrix} 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 \end{pmatrix}, \Delta &= \begin{pmatrix} 2 \\ -1 \\ 1 \\ -2 \end{pmatrix} \end{align*}\]i.e. Team 1 beat team 2 and 4 1-0 and tied team 3, and team 3 beat team 4 1-0. Note that the previous ratings add up to 0.
The new ratings are:
\[\begin{align*} r &= \begin{pmatrix} 1/3 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1/2 & 0 \\ 0 & 0 & 0 & 1/2 \end{pmatrix} \left( \begin{pmatrix} 0 & 1 & 1 & 1 \\ 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ 0 \\ -1 \end{pmatrix} + \begin{pmatrix} 2 \\ -1 \\ 1 \\ -2 \end{pmatrix} \right) \\ &= \begin{pmatrix} 1/3 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1/2 & 0 \\ 0 & 0 & 0 & 1/2 \end{pmatrix} \left( \begin{pmatrix} -1 \\ 1 \\ 0 \\ 1 \end{pmatrix} + \begin{pmatrix} 2 \\ -1 \\ 1 \\ -2 \end{pmatrix} \right) \\ &= \begin{pmatrix} 1/3 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1/2 & 0 \\ 0 & 0 & 0 & 1/2 \end{pmatrix} \begin{pmatrix} 1 \\ 0 \\ 1 \\ -1 \end{pmatrix} \\ &= \begin{pmatrix} 1/3 \\ 0 \\ 1/2 \\ -1/2 \end{pmatrix} \end{align*}\]The new ratings no longer add to zero.
Setting 3) Score differential capped at 7
In this case, AGD is no longer simply the difference between goals scored and goals yielded because this quantity can only take a maximum value of 7 per game. Instead, we need to define new variables
\[\begin{align*} \delta_g = \text{goals scored in game g} - \text{goals yielded in game g}\\ \tilde \Delta_i = \sum_{g \in \text{games played by team }i} t_7(\delta_g) \end{align*}\]where $t_\theta(\delta_g)$ is the truncated identity function, i.e. it is the identity when $\vert \delta_g \vert < \theta$ and equal to $-\theta$ when $\delta_g < -\theta$ and $\theta$ when $\delta_g > \theta$.
Our update rule becomes:
\[\begin{align*} r&=(diag(n))^{-1}(Sr^{(prev)} + \tilde \Delta) \end{align*}\]The change in rating for team $i$ is:
\[\begin{align} n_i(r_i-r_i^{(prev)})&=\tilde \Delta_i - \left(\sum_{g \in \text{games played by team }i} r^{(prev)}_i-r^{(prev)}_{\text{opponent in game g}}\right) \nonumber \\ &= \sum_{g \in \text{games played by team }i} \left(t_7(\delta_g) - \left(r^{(prev)}_i-r^{(prev)}_{\text{opponent in game g}}\right) \right) \end{align}\]The rule for whether your rating will increase or decrease is the same as before, except in the case of rating differentials greater than 7. In this case, when a team is ranked more than 7 points above its opponent, the game result is guaranteed to lower the rating of the higher ranked team, and raise the rating of the lower ranked team.
Result 3a) Goal difference needed for team $i$ to surpass team $j$
Say team $i$ is playing a game and needs to achieve rating higher than $r_j$. What is the score differential $\delta$ they need to achieve? First assume that team $i$ is not playing team $j$, and say that we know the current rating of team $i$ as $r_i^{(cur)}$. If team $i$ wants to be ranked above team $j$ after their game, then they must achieve a differential $\delta$ that satisfies:
\[\begin{align} t_7(\delta) > n_i \left(r_j - r_i^{(cur)} \right) - r^{(prev)}_{\text{opponent}} + r_i^{(cur)} \end{align}\]Proof:
Recall that
\[\begin{align*} (n_i-1)r_i^{(cur)}=\sum_{g \in \text{previous games played by team }i} \left(t_7(\delta_g) + r^{(prev)}_{\text{opponent in game g}} \right) \end{align*}\]Now,
\[\begin{align*} r_j&\lt \frac{1}{n_i}\left( t_7(\delta) +r^{(prev)}_{\text{opponent}}+(n_i-1)r_i^{(cur)} \right)\\ t_7(\delta) &\gt n_i r_j -r^{(prev)}_{\text{opponent}} - (n_i-1)r_i^{(cur)} \\ &= n_i \left(r_j - r_i^{(cur)} \right) - r^{(prev)}_{\text{opponent}} + r_i^{(cur)} \end{align*}\]$\blacksquare$
If the value on the right hand side is greater than 7, it is impossible for team $i$ to surpass team $j$ after this game. If it is less than -7, than team $i$ is guaranteed to remain ahead of team $j$. When the right hand side is between -7 and 7, team $i$ needs to achieve a minimum goal differential $\delta$. This goal differential increases when (all other things being equal):
- $\uparrow n_i$ : The number of games team $i$ has played is increased
- $\uparrow \left(r_j - r_i^{(cur)} \right)$ : The current rating difference between team $j$ and team $i$ is increased
- $\downarrow r_i^{(cur)}$ : The current rating of team $i$ is decreased
- $\downarrow r_{opponent}^{(prev)}$: The previous rating of the opponent is decreased
Now, say team $i$ is playing team $j$. Then if team $i$ wants to be ranked above team $j$ after their game, then they must achieve a differential $\delta$ that satisfies:
\[\begin{align} t_7(\delta)> \frac{n_ir^{(prev)}_{i} - n_j r^{(prev)}_{j} + n_i(n_j-1)r_j^{(cur)} - n_j(n_i-1)r_i^{(cur)}}{\left(n_j+n_i\right)} \end{align}\]Proof: \(\begin{align*} r_i &> r_j \\ \frac{1}{n_i}\left( t_7(\delta) +r^{(prev)}_{j}+(n_i-1)r_i^{(cur)} \right) &> \frac{1}{n_j}\left( -t_7(\delta) +r^{(prev)}_{i}+(n_j-1)r_j^{(cur)} \right) \\ t_7(\delta) &> \frac{n_i}{n_j}\left( -t_7(\delta) +r^{(prev)}_{i}+(n_j-1)r_j^{(cur)} \right) -r^{(prev)}_{j}-(n_i-1)r_i^{(cur)} \\ t_7(\delta) \left(1+\frac{n_i}{n_j}\right)&> \frac{n_i}{n_j}\left( r^{(prev)}_{i}+(n_j-1)r_j^{(cur)} \right) -r^{(prev)}_{j}-(n_i-1)r_i^{(cur)} \\ t_7(\delta) &> \frac{\frac{n_i}{n_j}r^{(prev)}_{i} - r^{(prev)}_{j} + \frac{n_i}{n_j}(n_j-1)r_j^{(cur)} - (n_i-1)r_i^{(cur)}}{\left(1+\frac{n_i}{n_j}\right)} \\ &= \frac{n_ir^{(prev)}_{i} - n_j r^{(prev)}_{j} + n_i(n_j-1)r_j^{(cur)} - n_j(n_i-1)r_i^{(cur)}}{\left(n_j+n_i\right)} \end{align*}\)
$\blacksquare$
If the value on the right hand side is greater than 7, it is impossible for team $i$ to surpass team $j$ after this game. If it is less than -7, than team $i$ is guaranteed to remain ahead of team $j$. When the right hand side is between -7 and 7, things the goal differential needed increases when:
- $\uparrow r_i^{(prev)}$: The team’s previous rating is increased
- $\downarrow r_i^{(cur)}$: The team’s current rating is decreased
- $\downarrow r_j^{(prev)}$: The opponent’s previous rating is decreased
- $\uparrow r_j^{(cur)}$: The opponent’s current rating is increased
The dependence on $n_i$ and $n_j$ is more complex.
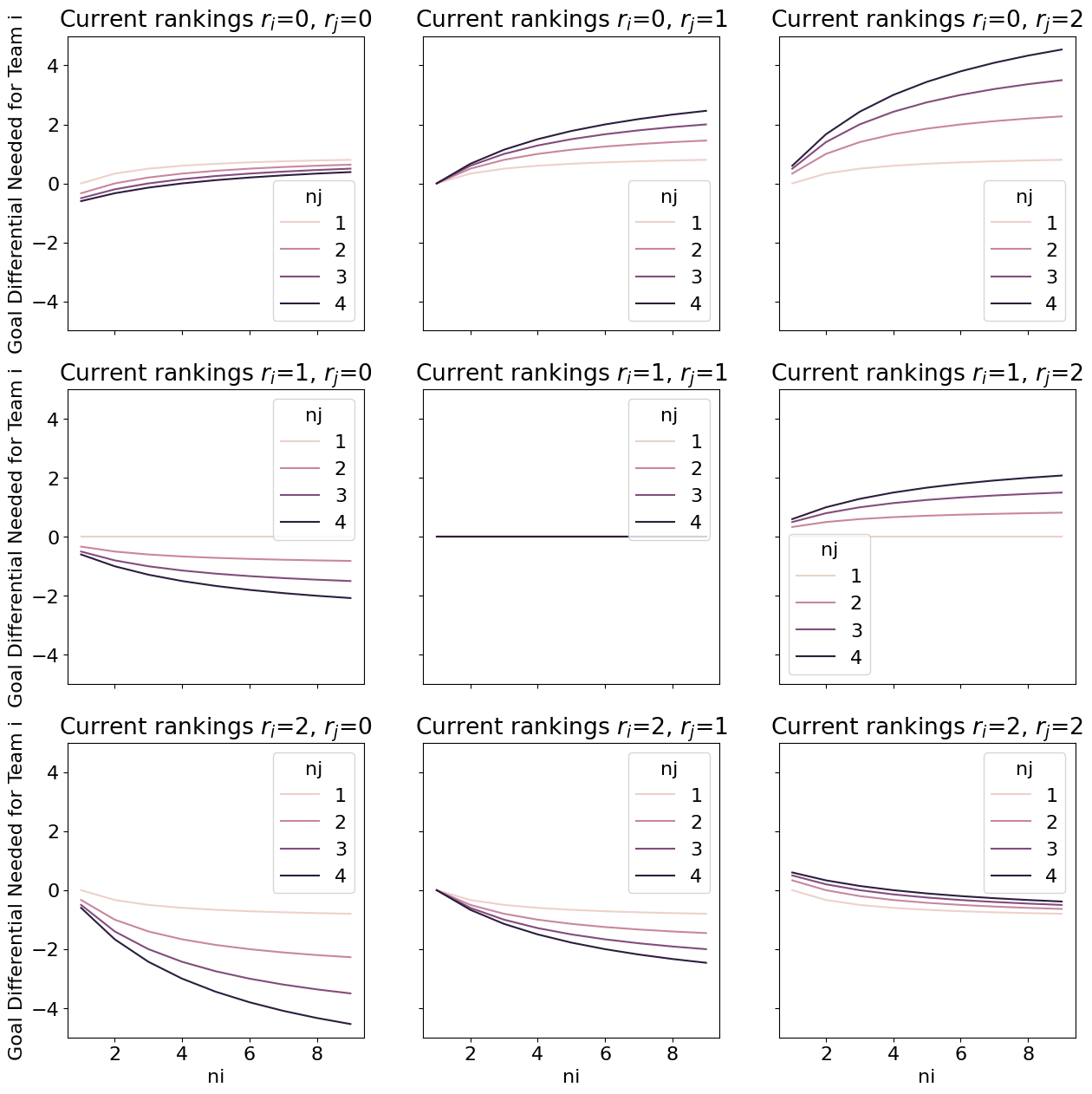
Empirically, when $r_i^{(cur)}>r_j^{(cur)}$, the team only needs to win in order to preserve their higher rating. When $r_i^{(cur)}<r_j^{(cur)}$, the goal differential needed increases when (all other things being equal):
- $\uparrow n_i$: Team $i$’s number of games played is increased
- $\uparrow n_j$: The opponent’s number of games played is increased
When the current ratings are equal, the difference between last year’s ratings and the current ratings matters. Even if the previous and current ratings of the teams are the same, if both teams have gotten worse, the team with more games needs to win, in order to counteract their longer slump.
Troubling Property of Formula
So far, our results put this rating system in a positive light. We have proven properties that we would want this system to have. However, a glaring weakness of this system is how it converges to ratings not equal to the previous year’s ratings.
Say that, while the previous year’s rankings are $r^{(prev)}$, the underlying strengths of the teams this year is given by some other vector $r^{(new)}$ where $r^{(new)} \neq r^{(prev)}$. If the teams play enough games, will this year’s rankings converge to $r^{(new)}$? The answer is, unfortunately, no.
Result 4) Simple scenario with weird result
Say there are two teams, team Good and Bad. Last year, team Good was rated 1 and team Bad was rated 0. Thus, we expect team Good to beat team Bad by a goal difference of 1. However, this year, team Good recruited some great players. They play team Bad $n$ times and they always win by a score of 2-0. What do you think the new rating difference will be? You can take $n$ to be as big as you want it to be.
It’s reasonable to expect that the new rating difference will be around 2, or, at least somewhere between 1 and 2. What if I told you the new rating difference is 3? Indeed
\[\begin{align*} \text{Team Good new rating}=\text{AGD} + \text{Sched} = 2 + 0 = 2 \\ \text{Team Bad new rating}=\text{AGD} + \text{Sched} = -2 + 1 = -1 \\ \end{align*}\]Last year team Good had a higher rating by 1, this year they always win by 2, but somehow their new rating is higher by 3.
Discussion
Recall that I made a couple assumptions about how the score of the schedule is computed. In particular, I assumed that the schedule score is computed from last year’s ratings, and only includes the games that a team has already played this season. This analysis will not necessarily hold up if those assumptions are not true.
However, under these assumptions we showed that:
- For a game with a rating differential less than 7, if the goal differential is equal to the rating differential, the teams’ ratings will not change (Equations 1,3,4).
- If all teams play the same number of games, the sum of their ratings remains unchanged (Equation 2), but this is not the case if teams play a different number of games.
- When a team wants a result to put them ahead of another team, the required game differential depends positively on the rating gap and the number of games they played and depends negatively on their current rating, and their opponent’s previous rating (Equation 5). If they are playing the team they want to surpass, then it also depends positively on their previous year’s rating, their opponent’s current rating, and the number of games their opponent has played (Equation 6).
- The formula fails to converge to new rating values even in a simple scenario (Result 4).
A future area of work could be to propose a modified system that has better convergence properties. At the very least, if the new game results follow, in expectation, some new set of ratings, $r^{(new)}$ we would hope that our formula, over time, converges on this vector.
Maybe I will look into that in the future, but for now I need to return to my actual work.
